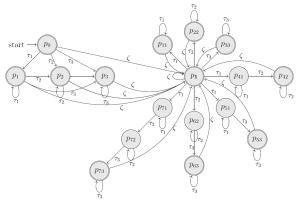
Motivated by statistical models with varying numbers of parameters, in the past decade there has been an interest in asymptotic phenomena for infinitely many objects such as ideals and algebras related by a group action. We can record detailed quantitative data for infinitely many related objects in a multivariate formal power series, which we call the equivariant Hilbert series. The rational form of these series, if it exists, is of interest as it can provide additional data about the objects in study. In searching for this rational form, we utilize theory of languages and their automata from computer science. For a language and a weight function on it, the sum of weights of words in the language is a multivariate formal power series. This series has a always rational presentation when the language satisfies certain rules determined by a directed graph on a finite number of nodes, commonly known as a regular language. The rational form can be easily computed via the graph. Now, given a family of related algebraic objects, we search for regular languages and weights on them such that their formal power series equals the equivariant Hilbert series for our related objects. The talk will be introductory and is based on is based on https://arxiv.org/abs/2204.07849 and https://arxiv.org/abs/1909.13026. No knowledge on Hilbert series or languages will be assumed.