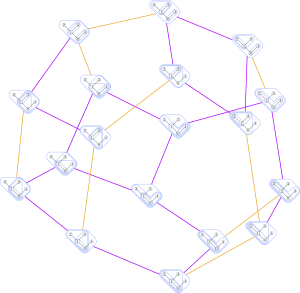
Two classical lattices are the Tamari lattice on bracketings of a word and the weak order on permutations. The Hasse diagram of each of these lattices is the oriented 1-skeleton of a polytope, the associahedron and the permutohedron respectively.

We examine a poset on bracketings of rooted trees whose Hasse diagram is the oriented 1-skeleton of a polytope called the operahedron. We show this poset is a lattice which answers a question of Laplante-Anfossi. These lattices provide an extremely natural generalization of both the Tamari lattice and the weak order.

No knowledge of lattices or polyhedral combinatorics is assumed.